盒卷积层

盒卷积层(Box Convolution Layer),想法来自于 Burkov, E., & Lempitsky, V. (2018) Deep Neural Networks with Box Convolutions. Advances in Neural Information Processing Systems 31, 6214-6224. 这篇论文
论文原址:https://papers.nips.cc/paper/7859-deep-neural-networks-with-box-convolutions
Github地址:https://github.com/shrubb/box-convolutions
简要介绍
使用积分图像计算的盒形滤波器长期以来一直是计算机视觉工具集的一部分。在这里,我们展示了一个以滑动方式计算盒滤波器响应的卷积层,这个卷积层可以在深度架构中使用,而在这种层中,滑动框的尺寸和偏移量可以作为端到端损失最小化的一部分来学习。关键的是,训练过程可以使这样一层中的盒卷积的大小任意变大,而不需要额外的计算成本,也不需要增加可学习参数的数量。由于它能够在较大盒卷积上集成信息,从而新层促进了信息的远程传播,并导致网络中下层单元接受域的有效增加。通过将新层加入现有的语义分割体系结构中,既可以提高分割精度,又可以降低计算成本和可学习参数的数量。
基本描述
为什么发明这种网络层:
因为:3×3卷积很小->导致接受域增长缓慢->导致层数变得很深。对于一些任务比较繁重的任务,我们不得不增加网络的层数以实现一些复杂的功能(在使用普通3×3卷积的条件下)。
或者我们使用dilated/deformable convolutions(典型的空洞和形变卷积),但是这些卷积容易产生人工痕迹,以及容易过滤掉高频信息。
或者我们采用”global” spatial pooling layers,但是限制比较多。
如何工作
盒卷积其实和深度可分离类似(i.e. Conv2d with groups=in_channels),但是拥有特殊的核,称为box kernels(中文名为..盒核?)。
盒核是一个矩形的平均滤波器。也就是说,过滤器的值是固定的和单位的!相反,我们学习每个矩形−其大小和偏移量的四个参数:
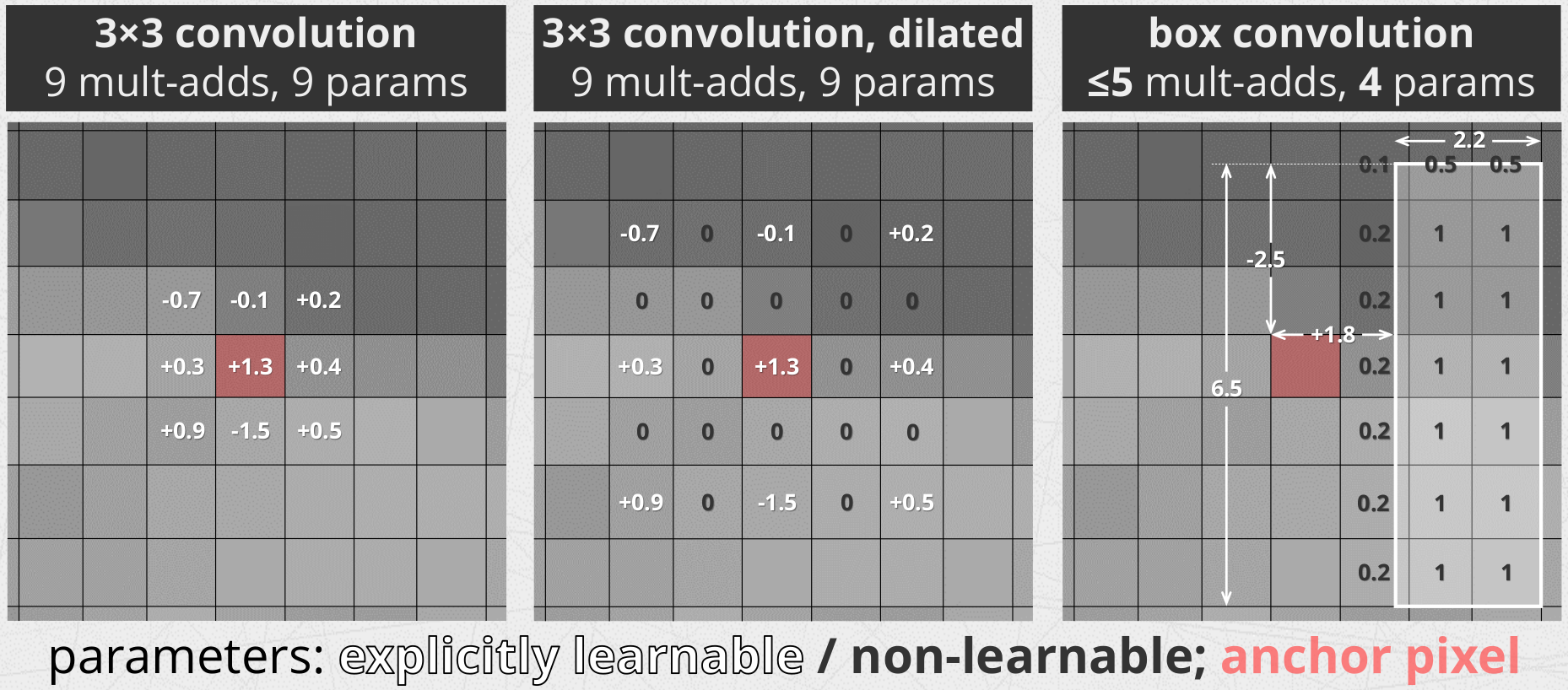
效果如何
将ENet.中经典的金字塔结构换一下:

整个神经网络会变得:
- 更加准确
- 更加快速
- 更加轻便
关于更加具体的消息请移步至相关页面~
